B树B+树AVL树红黑树
B树B+树AVL树红黑树
把这四颗 可爱 的树放在一篇博客来写就是因为他们都有一个共同点: 都是平衡树
传统的二叉树一旦发生倾斜那么就会退化为链表,这是二叉树最致命的缺点,所以就出现了如此多种的树,来提高数据查找的效率
B树 不同于二叉树,B树一个节点可能会有多颗子树,相当于是一颗多叉树,并且按照一定的规则来保持这种状态那么这个树就会维持的比较 矮胖,又因为B树有搜索树的性质所以二分查找起来速度就快了
B+树 就是B树的升级版,B+树和B树的不同在于叶子节点,B+树的每个叶子节点都会用链表连接起来,这样就支持 范围查找,B+树的叶子节点存放了所有数据和索引,而非叶子节点则只保存索引,这个非叶子节点保存的索引代表了子树中最小或则最大的索引,此索引是冗余的,一旦找到起始节点那么中间的节点就可以一起获取到,就不需要每次都从root节点开始遍历了
AVL树 是一颗平衡的二叉搜索树,一旦左右子树的平衡因子太大或则太小了那么就表示树已经失衡了,就会通过旋转操作来继续维持平衡因子到指定的值,所以旋转操作执行次数多的话也是比较耗时的
红黑树 和AVL树一样也是通过一定规则并且靠旋转、变色来维持树的平衡
在学习这些数据结构的时候不需要背规则,知道个大致原理即可
B树
又叫 多路查找树,和二叉树不同的是一个节点最多可以有多个子树
B树靠如下几个规则来保持树的平衡和矮胖:
根节点如果有孩子节点的话则至少有2个子节点
一颗
m阶的B树中所有节点的最大孩子节点数量<=m,所以最多包含m-1个关键字(因为孩子节点是在两个关键字之间进行插入的)中间节点关键字数量为k:
ceil(m/2)<=k<=m-1关键字之间是有序的,并且有搜索树的性质
所有叶子节点在同一层,也就是说根节点到所有叶子节点的距离都是一样的
B+树
B+树就是在B树的基础上对叶子节点进行了改进,将所有的叶子节点都用链表连接起来,B+树的只在叶子节点保存数据,其他节点保存索引值
B+树和B树的区别如下:
- 子树数量和关键字数量一致(B树中子树数量比关键字数量多1)
- 叶子节点使用链表连接
- 非叶子节点会存放冗余的索引,叶子节点会存放具体的值和所有索引,所以非叶子节点有值重复(而B树所有节点都是唯一的)
因为B+树的所有叶子都使用链表连接,所以B+树支持范围查找,只需要找到起始节点即可
AVL树
- 左旋
- 右旋
- 左右旋
- 右左旋
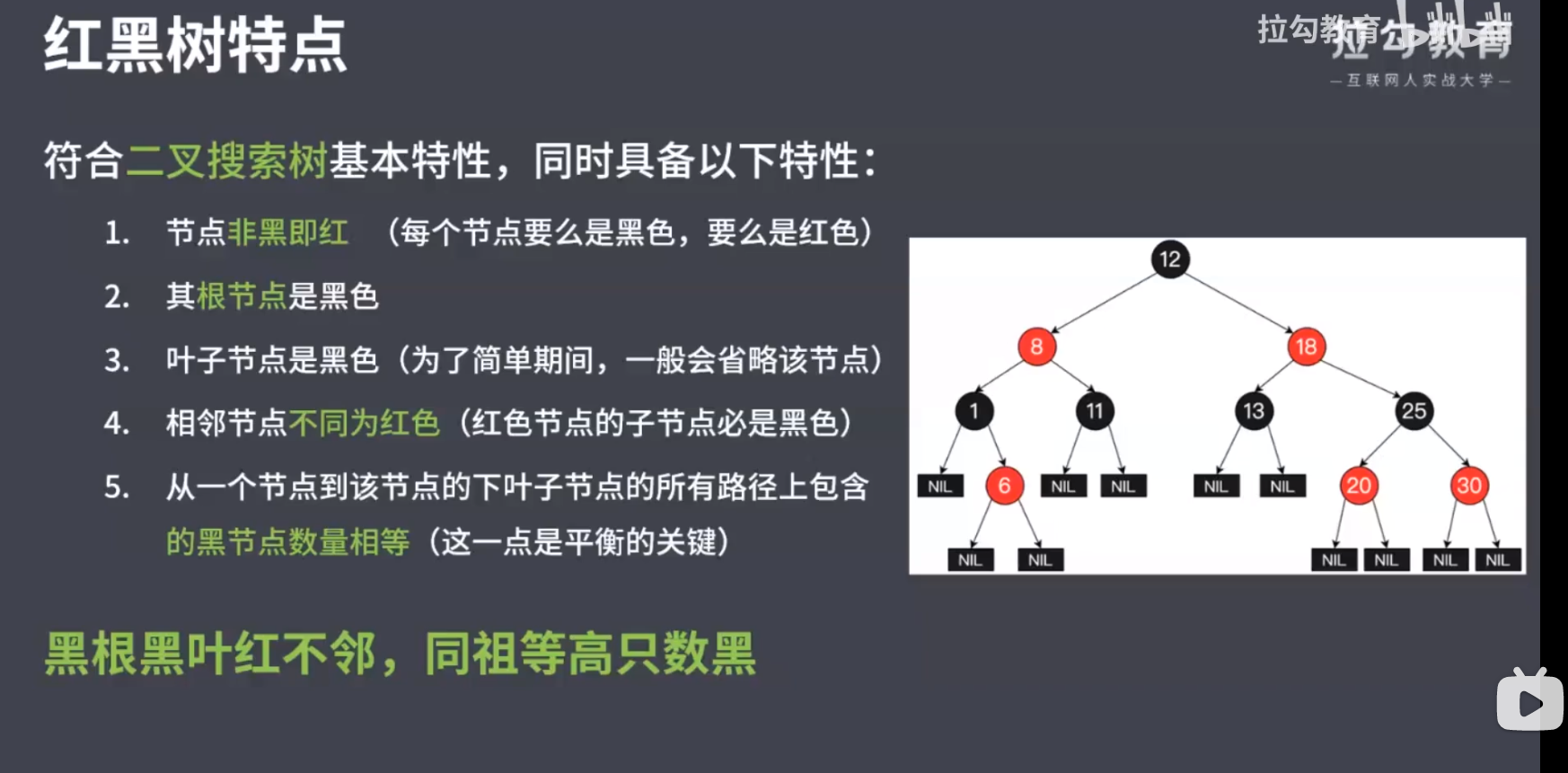
红黑树
- 节点非黑即红
- 根节点必须是黑色
- 叶子节点是黑色,一般省略叶子节点
- 相邻节点不能都为红色(红色节点的子节点或则父亲必须是黑色)
- 从一个节点出发的任意一条路径下的黑色节点数量相等
参考
B树-王道考研视频 【讲的很好】
2020B站最详细红黑树结构-二叉树-哈希-B+树-HASH-平衡算法
MYSQL核心底层原理大盘点!看完心里有B树了吗? 【InnoDB讲的很好】