完全二叉树和满二叉树

满二叉树

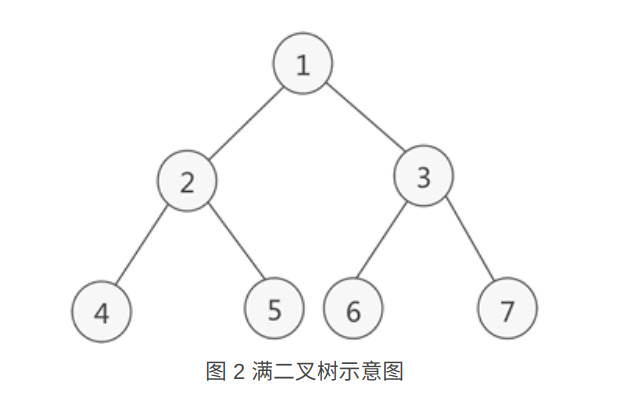
如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树

满二叉树有如下几个性质:

1. 满二叉树第i层节点的个数2^(i-1)

2. 深度为n的满二叉树必须有2^(n)-1个节点，叶子节点有2^(n-1) (也就是最后一层的节点数量)

3. 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树

4. 具有 n 个节点的满二叉树的深度为 log2(n+1)

5. 第i个节点的左右孩子分别为i*2+1 i*2+2 (孩子节点从0开始算起，如果孩子节点从1开始算起的话就是i*2 i*2+1 )

6. 第i个节点的父亲节点i/2-1 ，如果从1开始算起就是i/2

​

完全二叉树

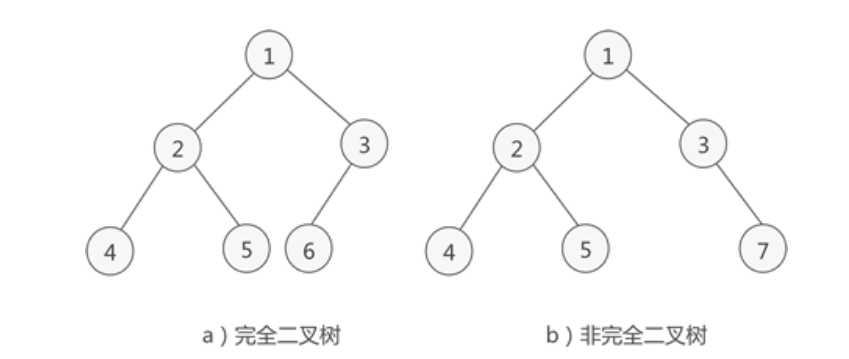
结点依次从左到右分布，中间无法断开，则此二叉树被称为完全二叉树，完全二叉树适合用数组来存储

1. 第i个节点的左右孩子分别为i*2+1 i*2+2 (孩子节点从0开始算起，如果孩子节点从1开始算起的话就是i*2 i*2+1 )

2. 第i个节点的父亲节点i/2-1 ，如果从1开始算起就是i/2

注意上面的计算要注意范围

堆就是用完全二叉树来实现的