十大排序算法
目录
O(n^2)排序算法
适合小规模数据排序
冒泡排序
- 稳定排序
- 最好时间复杂度:
O(n)基本有序状态,进行1次冒泡 - 最坏时间复杂度:
O(n^2)逆序状态,需要进行n次冒泡 - 平均时间复杂度:
O(n^2) - 空间复杂度:
O(1)
func BubbleSort(arr []int) {
flag := true
for i := 0; i < len(arr); i++ {
for j := 0; j < len(arr)-i-1; j++ {
if arr[j] > arr[j+1] {
flag = false
arr[j], arr[j+1] = arr[j+1], arr[j]
}
}
if flag {
break
}
}
}
插入排序
- 稳定排序 只有元素相同不会进行交换
- 最好时间复杂度:
O(n)基本有序状态 - 最坏时间复杂度:
O(n^2)逆序状态 - 平均时间复杂度:
O(n^2) - 空间复杂度:
O(1)
将数组分成两个区间: 有序区间、无序区间 然后寻找插入位置,算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束
func InsertSort(arr []int) {
for i := 1; i < len(arr); i++ {
v := arr[i] //待插入的值
j := i - 1 //搜索已经排好序的区间 寻找插入位置
for ; j >= 0; j-- {
if arr[j] > v {
arr[j+1] = arr[j]
} else {
break
}
}
arr[j+1] = v
}
}
选择排序
- 不稳定排序 比如
5 8 5 2 9两个相同的5会发生位置交换 - 最好时间复杂度:
O(n^2) - 最坏时间复杂度:
O(n^2) - 平均时间复杂度:
O(n^2) - 空间复杂度:
O(1)
每次选择剩余排序区间中最小(大)的元素放入排序好的区间的最后一个位置中
func SelectionSort(arr []int) {
for i := 0; i < len(arr); i++ {
min := i
for j := i + 1; j < len(arr); j++ {
if arr[j] < arr[min] {
min = j
}
}
arr[i], arr[min] = arr[min], arr[i]
}
}
O(nlogn)
适合大规模数据排序
希尔排序
- 不稳定排序
- 最好时间复杂度:
O(n)增量为1的时候就已经是全部有序了 - 最坏时间复杂度:
O(n^2)每次分组都不会发生交换,增量为1才发生交换 - 平均时间复杂度:
O(n^1.3) - 空间复杂度:
O(1)
又叫 缩小增量排序 插入排序的增强版本,因为插入排序在数组大多数都是有序的情况下效率较高,所以希尔排序就是根据这个规则先把数列进行分组,组内不停使用插入排序,直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换) 增量不断递减
比如有一个数组 `[3,21,5,4,3,2,90,8]` 8个元素 我们可以用一个序列来表示增量:n/2、(n/2)/2、...、1,每次增量都/2
增量为4: [3,3] [21,2] [5,90] [4,8] -> [3,3,2,21,5,90,4,8]
增量为2: [3,3,2,21] [5,90,4,8] -> [2,3,3,21] [4,8,5,90]
增量为1: [2,3,3,21,4,8,5,90] -> [2,3,3,4,5,8,21,90]
func ShellSort(arr []int) {
for step := len(arr) / 2; step >= 1; step /= 2 {
for i := step; i < len(arr); i++ {
v := arr[i]
j := i - step
for ; j >= 0; j -= step {
if arr[j] > v {
arr[j+step] = arr[j]
} else {
break
}
}
arr[j+step] = v
}
}
}
归并排序
- 稳定排序
- 最好时间复杂度:
O(nlogn) - 最坏时间复杂度:
O(nlogn) - 平均时间复杂度:
O(nlogn) - 空间复杂度:
O(n)递归栈空间
假设对 `n` 个元素进行归并排序需要的时间是 `T(n)` ,那分解成两个子数组排序的时间都是: `T(n/2)`
`merge() 函数`合并两个有序子数组的时间复杂度是 `O(n)` ,所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
T(n)=2T(n/2)+n
=2*(2*T(n/4)+n/2)+n
=4*T(n/4)+2*n
=4*(2*T(n/8)+n/4)+2*n
=8*T(n/8)+3*n
=8*(2*T(n/16)+n/8)+3*n
=16*T(n/16)+4*n ........
=2^k*T(n/2^k)+k*n
-------------------------
T(n) = 2^kT(n/2^k)+kn
-------------------------------
当`T(n/2^k)=T(1)`时,也就是`n/2^k=1`,我们得到`k=log2n`
我们将k值代入上面的公式,得到`T(n)=Cn+nlog2n`
如果我们用大O标记法来表示的话,`T(n)=O(nlogn)`
//分治思想
func MergeSort(arr []int, temp []int, left, right int) {
if left >= right {
return
}
mid := (left + right) / 2
MergeSort(arr, temp, left, mid)
MergeSort(arr, temp, mid+1, right)
//两边数组已经有序
if arr[mid] < arr[mid+1] {
return
}
//复制要合并的数据
for i := left; i <= right; i++ {
temp[i] = arr[i]
}
i1 := left //左边的开始位置
i2 := mid + 1 //右边的开始位置
//归并
for i := left; i <= right; i++ {
if i1 <= mid && (i2 > right || temp[i1] < temp[i2]) {
arr[i] = temp[i1]
i1++
} else {
arr[i] = temp[i2]
i2++
}
}
}
快速排序
- 不稳定排序
- 最好时间复杂度:
O(nlogn)pivot支点选平均值的时候 - 最坏时间复杂度:
O(n^2)pivot支点选最大或则最小的时候,退化为冒泡 - 平均时间复杂度:
O(nlogn) - 最优空间复杂度:
O(logn)递归的栈空间,每次平分,递归树为平衡二叉树 - 最差空间复杂度:
O(n)退化为冒泡,递归树为单边二叉树
快速排序主要解决的问题就是:
- 确定pivot
- 如何将pivot放到正确的位置
O(n)
计数排序
- 稳定排序
- 时间复杂度:
O(n+k),k 指的是数据量 - 空间复杂度:
O(n+k)
适合数据量小,并且数据范围密集紧凑(正太分布),如果数据量大并且分布不均匀很稀疏则效率不高,使用桶排序或则其他排序如快排效率高点
func CountSort(arr []int) {
min, max := 0, 0
for _, v := range arr {
if v > max {
max = v
}
if v < min {
min = v
}
}
counter := make([]int, max+1)
//记录每个数出现的次数
for _, v := range arr {
counter[v]++
}
i := 0
for j := min; j <= max; j++ {
for counter[j] > 0 {
arr[i] = j
i++
counter[j]--
}
}
}
桶排序
- 时间复杂度:
O(n+k),其中n为待排序的元素的个数,k为桶的个数 - 空间复杂度:
O(k)k是桶的个数
同计数排序思想差不多,只不过这个是以 数值区间 来排,计数排序适合于数据小紧凑的数据,而桶排序适合于大量数据的排序
func BucketSort(arr []int, bucketSize int) {
min, max := 0, 0
for _, v := range arr {
if v > max {
max = v
}
if v < min {
min = v
}
}
diff := (max - min + 1) / bucketSize
bucket := make([][]int, bucketSize)
//分别将数据放入对应区间的桶中
for i := 0; i < len(arr); i++ {
pos := (arr[i] - min) / diff //桶大小可能最后一个会多点 会有不整除的情况
if pos >= bucketSize {
pos = bucketSize - 1
}
bucket[pos] = append(bucket[pos], 0) //扩容一个空间
j := len(bucket[pos]) - 2
//放入的时候采用插入排序法 让桶内元素保持有序
for ; j >= 0; j-- {
if bucket[pos][j] > arr[i] {
bucket[pos][j+1] = bucket[pos][j]
} else {
break
}
}
bucket[pos][j+1] = arr[i]
}
//从每个桶里面取出数据 然后有序的放入原数组
i := 0
for pos := 0; pos < bucketSize; pos++ {
for _, v := range bucket[pos] {
arr[i] = v
i++
}
}
}
基数排序
func Max(arr []int) int {
max := arr[0]
for _, v := range arr[1:] {
if max < v {
max = v
}
}
return max
}
func MaxBit(arr []int) int {
max := Max(arr)
c := 0
for max > 0 {
max /= 10
c++
}
return c
}
func RadixSort(arr []int) {
maxBit := MaxBit(arr)
bucket := make([][]int, 10) //开10个桶
size := len(arr)
power := 1
for i := 0; i < maxBit; i++ {
for j := 0; j < size; j++ {
pos := (arr[j] / power) % 10
bucket[pos] = append(bucket[pos], arr[j])
}
index := 0
for j := 0; j < 10; j++ {
for len(bucket[j]) > 0 {
arr[index] = bucket[j][0]
bucket[j] = bucket[j][1:]
index++
}
}
power *= 10
}
}
堆排序
基于数据结构 堆 来实现排序,堆 我会再写一篇文章来概述,代码请访问 https://github.com/biningo/algorithm-play
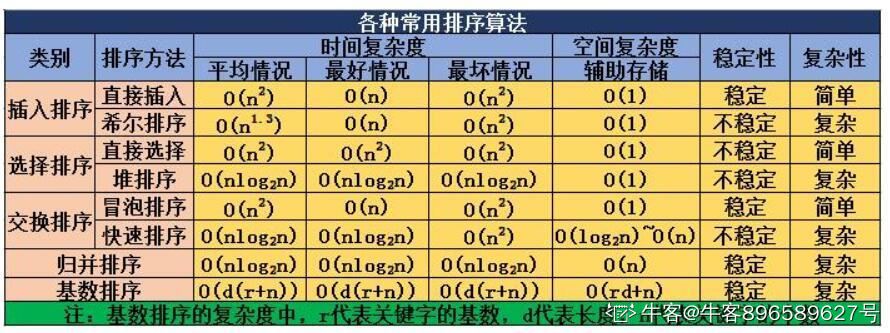
总结
参考
https://juejin.cn/post/6844903863288332302#heading-7
https://juejin.cn/post/6844904007182319624 【希尔排序】
https://github.com/sisterAn/JavaScript-Algorithms/issues/75 【希尔排序】